1. Confirm a candidate model with observations

Flat-earthers are folks who strongly hold the view that the earth is not a spheroid with an equatorial diameter of 12756 km and a polar diameter of 12713 km that rotates on its polar axis once a day. Not all of them actually think the earth is flat, but most do have a picture in mind that resembles one published in 1849 by a gentleman named Rowbotham. In this model, the earth’s surface is a disk with the north pole at its center. Antarctica is spread out to form the edge of the disk and is often referred to as the ice wall.

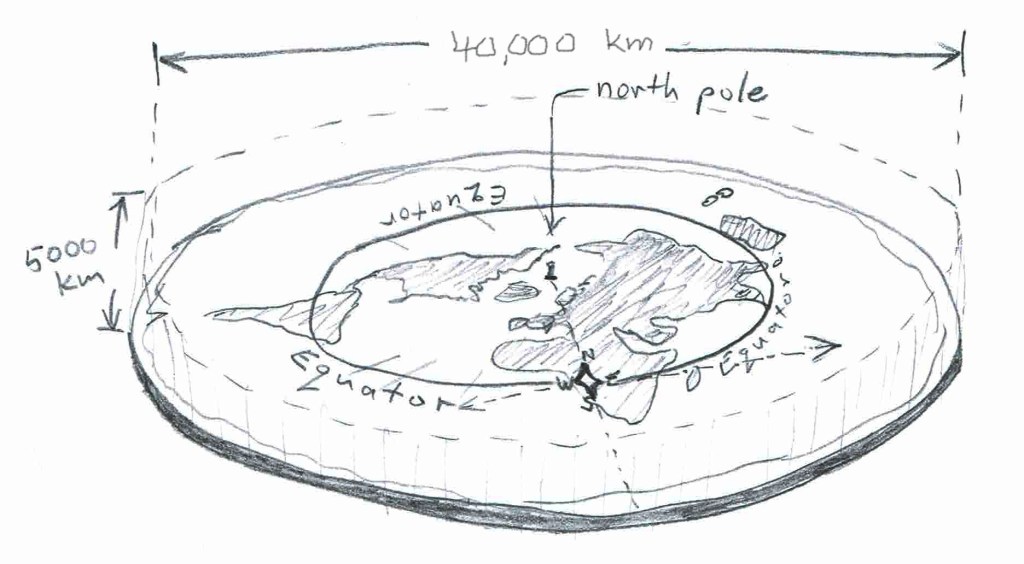
This model places the sun and moon about 4800 km above the disk and the stars a smidgeon higher in altitude, about 5000 km. These additional disks spin around the north pole about once per day.

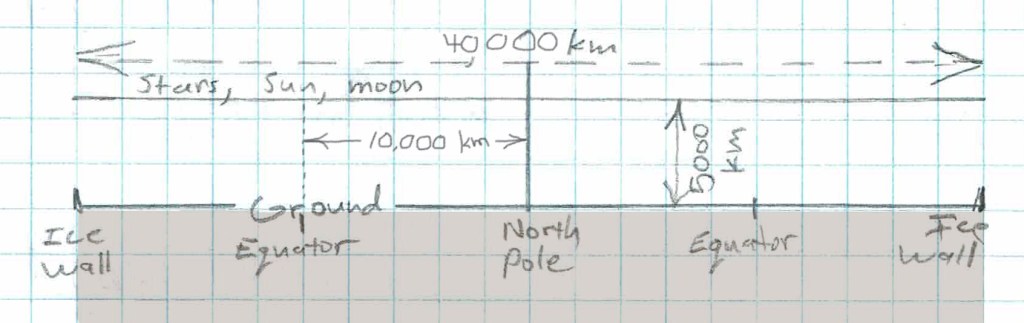
The sun rotates in circles above the equator, tighter circles in northern hemisphere summer and circles of larger radius during the winter months.

This picture makes many predictions. Many of those predictions are easy to measure. And yet, flat-earthers never measure them.

For those flat-earthers who are sincere and not driven by religious zeal or paranoia, here are a few easily confrontable items that, somehow, flat-earthers never get around to testing.

2. Observe a lack of a south celestial pole

If one screws an old-fashioned film camera on a tripod facing north at night and takes a long exposure, one ends up with star trails like this.

The center of apparent motion is called the north celestial pole, an extension of the earth’s rotation axis in the spherical earth model. Note Polaris, a bright star slightly displaced from the apparent center of motion. In the round earth model, a south celestial pole is inevitable.

There happens to be no bright star near the south celestial pole.

How can one see this? (1) Travel to the southern hemisphere with a camera capable of taking long exposures. You could also phone up a buddy who lives in Australia and ask for such a picture. (2) Take a long exposure. On any clear night. Facing south. The photo above was exposed for several hours, but the effect can easily be seen after ten minutes. Also, while taking a photo is great for instant gratification, the same job can be done by measuring altitudes and azimuths (see next section) for prominent stars in the area.

Take a glance at the flat earth model. It contains only a north celestial pole. In the flat earth model, stars in the sky to the anti-north (south) direction travel sideways. The very existence of a south celestial pole negates the Rowbotham model. (I label the model “Rowbotham” because flat-earthers have a lot of models, but this one fact negates all of the popular ones.)

And that’s a thing that flat earthers never do: acknowledge the existence (and implications!) of the south celestial pole.

3. Triangulate

In the flat earth model the sun hovers in the air at some constant altitude and travels in a round path near the equator of the earth, itself a circle in the flat earth model. Since the sun is so near, it should be easy to triangulate and find its altitude.

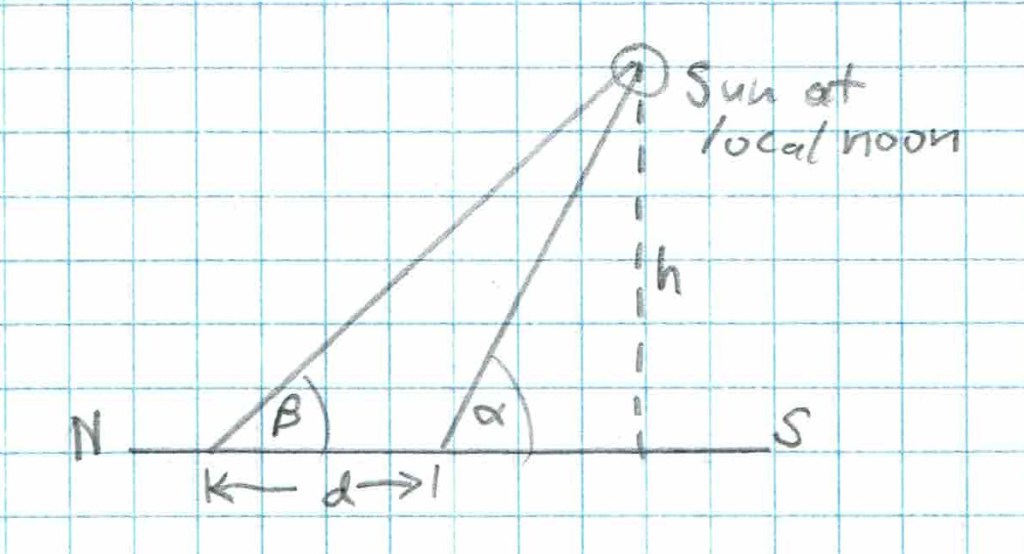
Suppose you had two observers on a north-south line separated by a distance d. We’re assuming a flat earth for this picture, and we are also waiting until the sun is at local noon. That is, crossing the meridian, the plane that contains the N and S compass points, the zenith, the nadir, and, by definition, the sun at local noon. The figure above is in the plane of the meridian, with N and S directions marked. The goal is to measure h, the height of the sun in kilometers (or any other distance unit). To do it, we have two stations on a N-S line, and we measure the altitude of the sun above the S compass point, where altitude is the angle of an object above the horizon. The measured quantities are the two altitude angles and the distance between them, gotten from a highway map. High school trigonometry is sufficient to answer the problem.

I suppose another thing flat-earthers never do is learn trig, but all this requires is two applications of the Law of Sines. The Law of Sines applies to any triangle with angles A, B, and C, and lengths of the opposing sides a, b, and c.

and it’s a lovely set of ratios

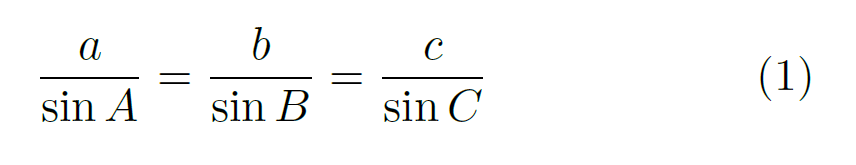
involving the sine trig function. Let’s add a few labels to our diagram.

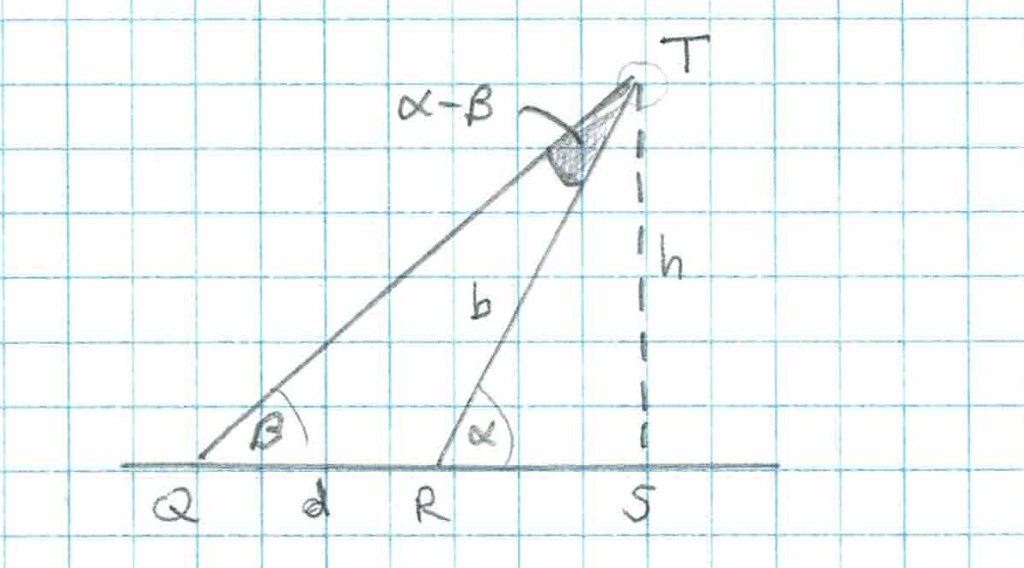
QRST are labels for the corners. Angle QST is a right angle. Because the interior angles of a triangle sum to 180, you can deduce that the skinny angle is the difference of the measured angles alpha and beta. Side b is opposite angle beta, so you can apply the Law of Sines to the skinny triangle (triangle QRT).

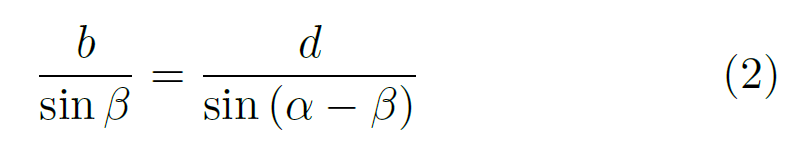
Allow me to rearrange that for later convenience.

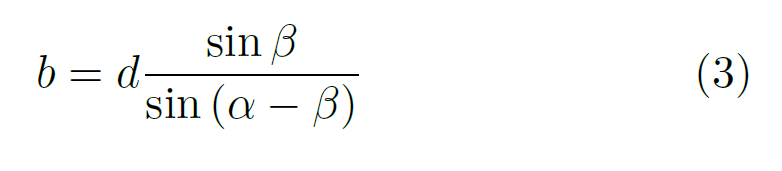
One can apply the Law of Sines again to the big triangle QST.

Conveniently,

so we have

Look! It’s an equation for h, the physical height of the sun. But we need to eliminate the length b from it. We do that by substituting equation (3) for b into equation (6).

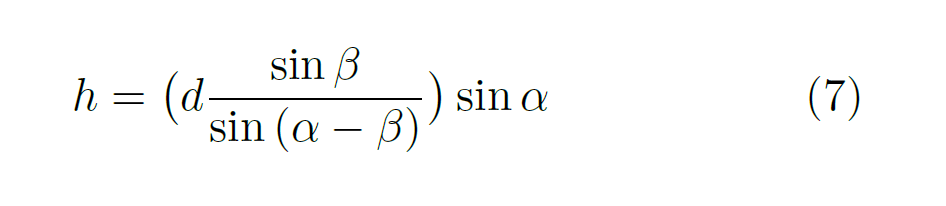
with a slight spring tidy to make the equation as neat as possible.

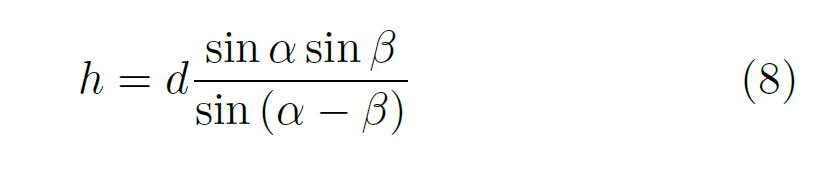
The height of the sun h will be in whatever units the distance d is measured in. The only quantities on the right-hand side of the equation are the known altitude measurements and distance between stations.

Altitude angles can be measured with a pair of hinged sticks … but a theodolite is built for the job. Surveyors use them for triangulation. They’ve got really accurate digital ones, now, but I’d recommend a flat-earther get an old-fashioned transit theodolite like this one because of its lack of electronics.

With practice, accuracies can reach 1/3 arcminute with an instrument like this. What accuracies are required? Let’s take an example. A couple of populous cities nearly N-S of each other are New Orleans (longitude 90.1 degrees W, latitude 30.0 degrees north) and St. Louis (longitude 90.2 degrees W, latitude 38.6 degrees north). They’re 950 km apart (I rounded a bit). To further simplify my example, let’s assume it’s an equinox, so the sun is directly over the equator, making it 3330 km south of New Orleans. Consulting the flat earth model, the sun’s height is 4800 km, so h = 4800. Consulting our diagram, distance RS is 3330 km, and d = 950 km.

The Pythagorean theorem yields distance RT = b = 5842 km, and distance QT = 6431 km. From there, sin(alpha) = h/b, so alpha = 55.25 degrees. Similarly, sin(beta) = h/QT, so beta = 48.28 degrees. For this example, alpha-beta = 6.97 degrees. If you really could measure solar altitudes to 1/3 arcminute (0.0055 degrees) your accuracy would be 0.08%, which is spectacular. In reality, some real-world issues like deciding on the moment of local noon and dealing with the finite disk of the sun will lessen the accuracy. (Never look at the sun, by the way! Securely tape some welder’s glass over the theodolite objective.)

What will you find? In the round-earth model (because the sun is very distant), you will find that alpha = 90 degrees minus the latitude of the observing station. Likewise, beta = 90 degrees minus the latitude of the observing station. For the above example, we’d expect alpha-beta = 38.6 – 30.0 = 8.6 degrees, which should be a measurable difference from the flat-earth, h=4800 model.

But wait. The two models diverge much more strongly when you stray farther from Rowbotham’s homeland. Suppose your two stations were (1) at the equator, and (2) at the north pole. Round earth says alpha-beta = 90 degrees.

Let’s work out the flat earth answer. In that case, alpha = 90 degrees, d = 10000 km, and we only need one right triangle to arrive at sin(beta) = h/QT = 4800/11090, or beta=25.6 degrees, so that alpha-beta = 64.4 degrees, an angle not easily confused with 90 degrees.

The prediction from round-earthers is that flat-earthers will never arrive at a consistent altitude for the sun. Any particular pair of N-S observing stations will triangulate a consistent altitude for the sun, for any season, but pick a different pair of stations and the answer will differ. Note that the sun can’t be in two places at once.

This could be checked with a theodolite (or a pair of hinged yardsticks taped to a protractor) by several well-separated observers connected by telephone. It would cost almost nothing and it would take no more than a sacrificed lunch hour. And yet, flat-earthers never do it.

4. Track the sun

In Figure 1, I drew a little compass rose on the Congo in Africa. Note that the east-west line is a tangent to the equator. This is true for any equatorial observing station.

In the flat earth model, again simplifying to an equinox date, the sun travels above the equator line. Any equatorial observer will see the noon sun directly overhead, and a vertical stick will cast no shadow. Both round and flat models agree on that point.

In the round earth model the sun rises directly in the east and sets directly in the west. A stick’s shadow never strays from the east-west line. Take a glance at the flat disk model again. The sun hovers over the equator, which is a circle in that model. Except for the moment of noon, the sun is always north of the east-west tangent line.

So, except for the times near local noon, sunlight should always fall on the north side of a flat sheet, such as, literally, a sheet hung on a clothesline, as long as the clothesline string is oriented east-west. For the most part, the shadow cast by a vertical stick will point south in the flat earth model.

Flat-earthers should check to see that it does. But they never do.

5. Compute an angular velocity

Consider the sun’s movement in a flat earth model. It cruises along at constant altitude and with a constant speed. Its path curves around the north pole, but let’s suppress that detail for the moment and pretend it travels in a straight line. The sun’s actual physical velocity is a constant but its angular velocity in degrees per hour will lessen as it distances itself from the observer, say, in the afternoon.

Let theta represent the zenith angle of the sun (angle between the sun and zenith). The angular velocity is the number of degrees traversed by the sun over some convenient unit of time. Sparing you about 6 lines of algebra, the geometrical compression is

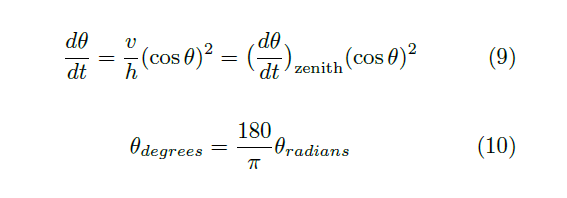
where v is the space velocity of the sun, and h is the sun’s height. The first half of equation 9 will be in radians units (SI units: radians per second), so be aware of the units change given in equation 10 since half a circle is 180 degrees and pi radians. The maximum angular velocity will be measured when the sun is near zenith and falls off from there.

For example, at zenith angle = 45 degrees, the angular velocity has dropped to half of its zenith value. At 60 degrees the angular velocity has dropped to a quarter of its zenith value. At 75 degrees from vertical, the angular velocity has dropped to less than 7 percent of its zenith value. This is not a subtle effect.

A shadow observatory (e.g., a plumb bob to locate zenith thumbtacked to a protractor) is the safe way to collect data. If the flat earth model is valid, the angular speed of the sun will be highest at noon and will progressively slow down as the sun westers.

Can some flat-earther spare a sunny afternoon to fill a spreadsheet with zenith angles? Apparently not.

(p.s., this works for stars, too.)

6. Observe rockin’ sunspots

Figure 9. A pair of visible-light solar images I snagged from the National Solar Observatory. Since we are near solar maximum, there are plenty of sunspots to view.

Suppose you were a flat-earther in the USA and you had a flat-earther buddy in Belgium. It’s morning for you and afternoon for your buddy, so the sun is hovering somewhere over the Atlantic Ocean. Since the two observers are seeing the sun from different perspectives, they should see something akin to the above pair of pictures. The USA observer should see more of the western half of the solar sphere (left image) while the Belgian should see more of the eastern portion (right image).

And 9 hours later, the USA observer’s sun should rotate until he or she observes what the Belgian saw 9 hours earlier.

These observations require a small telescope equipped with a solar filter, or binoculars similarly filtered, so there is a modest monetary cost here. Still, a lot of folks own telescopes, so this is a straightforward observation to make. It’s interesting how flat-earthers never make it.

7. Measure angular diameters

Since we’ve sneakily slipped telescopes into the conversation, how about also buying a reticle eyepiece? That’s a fantastic trick to put an angular scale atop your image, like telescopic gun sights do. It allows one to measure angular sizes, meaning the angular diameters of the sun, the moon, and many planets, or the separation between pairs of stars. The sun is half a degree across … Oops, sorry. I accidentally slipped in some round-earther bias in there. In the round earth picture, the sun is 150 million km away and varies in angular size between 31 1/2 and 32 1/2 arcminutes due to the 0.015 eccentricity of the earth’s orbit. But let’s go back to the flat earth picture.

I assume that flat earthers assume that the sun is of constant size and shaped like a ball. The sun is 4800 km above an equatorial observer at noon on an equinox, but that’s its close approach. It gets farther from there. Suppose it westers until it reaches a zenith angle of 45 degrees, around 3 p.m. Its new distance (via the Pythagorean theorem) is square root(2) = 1.41 bigger, or 6788 km. Angular diameters go as one over distance, so its angular diameter will have shrunk by 41% compared to its noontime size.

That’s quite a large difference! I wonder why no flat earthers have ever bought a reticle eyepiece and solar filter and made that observation.

(p.s., Separations between stars will also behave this way in the Rowbotham model, and also the angular diameters of the moon and fully resolved planets like Jupiter.)

8. Contemplate the elegant simplicity of an equatorial telescope mount

Imagine a telescope set up at the north pole. The sky wheels about the north celestial pole (NCP) which lies exactly at zenith. If your telescope mount revolved at the rate of 1 full rotation per sidereal day, it could compensate for the wheeling motion. An object in the eyepiece would stay there as the telescope tracks. It is this philosophy that drove the invention of the equatorial mount.

The beauty of it is that it works anywhere on earth. Align the polar axis of the telescope with the NCP or SCP and supply it with a very slow motor (called a clock drive). There’s a clutch, usually a pair of nylon disks, so that the operator can slew to different sky objects. The other axis is called the declination axis. In Fig. 10, the declination axis holds the telescope at one end and counterweights at the other. When properly aligned, an equatorial telescope will “sit” on an object all night.

Whoops, there I go again, inserting bias, for no reason other than I often operate a telescope with an equatorial mount and I can “sit” on a star or planet for hours without it drifting out of the eyepiece, whose view angle is around 25 arcminutes.

But the point is that an equatorial mount does not function in a flat earth picture, except at the north pole. Once the telescope is moved off that central axis, nothing so simple as a slow motor driving a shaft can follow the motions of the stars. The stars in Figure 1 are fixed relative to one another, and the lot of them rotate like a turntable, hovering 5000 km above the ground. An off-center telescope mount pointing up will have to deal with non-concentric motions as the clock drive spirals around a circle different than the sky’s. An off-center telescope mount tilted to point at the NCP will run into the non-constant angular velocities from section 5, above, plus geometric foreshortening where circles seen obliquely look like ellipses. Whatever star you’re targeting will glide away, to appear in your eyepiece again only after 24 hours.

Flat-earthers should genuinely worry that the most observer-friendly telescope mount¹ functions. It tracks stars, yet it shouldn’t under the flat earth hypothesis.

9. Call foul on the lame lunar eclipse explanation

The sun and moon never set in the Rowbotham model. They just stay at 4800 km altitude. If one observer is placed at the far lower left of Figure 2 (at the edge/ice wall) and the sun is placed over the farther-side equator (that is, the farthest away from the sun an observer can get), the sun is still 17.7 degrees above the horizon.² It should be daytime. However, flat-earthers say that the sun beams its light as if it was wearing a lamp shade, so it’s night.

Objection one: What lamp shade? How in tarnation does that even work when the sun is a spherical isotropic emitter?

Objection two: I see the sun approach the horizon a lot closer than 1.7 fists. I see the sun rise and set frequently, often from locations with excellent horizons.

I know the section is about eclipses, but to get there we have to somehow swallow the unseen lamp shade hypothesis. The lamp shade is important in the flat earth model because it causes night. The sun’s pool of light moves around the disk, and it’s night for an observer outside the irradiated zone.

Ergo, the sun beams no light horizontally.

Ergo, the moon, at a similar altitude as the sun, cannot be bathed in sunlight.

But it is, because we see it. And I’m pretty sure flat-earthers believe that it’s reflected sunlight that illuminates the moon. (Good, because if you take a spectrum of moonlight, it’s basically a solar spectrum.)

So now we’re left with a hood on the sun, but with a strategic sideways hole in the hood that points to the moon and illuminates it. I hope you, dear reader, can detect the piling on of additional arbitrary model structures.

Solar eclipses can, qualitatively at least, arise in the flat earth model if the moon crosses below the sun and casts a shadow on the ground. This should happen every new moon, but we’ll let that one slide for now.

Lunar eclipses, on the other hand, simply do not arise in the Rowbotham model. The earth cannot interpose itself between the sun and the moon. Modern flat-earthers, therefore, have added a “shadow object” to the model. Conveniently, like the solar hoodie, this shadow object is itself undetectable.

Objection three: An invisible object of unknown motion and composition that only semi-appears when it is needed to cast a circular shadow on the moon on the occasions of lunar eclipses.

So that’s the ninth thing flat-earthers never do: object to the convoluted band-aids necessary to prop up easy naked-eye lunar observations. To recap: the sun beams light directionally even though its spherical. This light goes downward except when flat-earthers need it to go sideways to illuminate the moon, but never sideways and slightly down, because that would bathe the disk world in perpetual sunlight. The somehow-illuminated moon is occasionally blotted out, but only during full phase, by an invisible shadow object.

A hallmark of science is to discover simple models that explain lots of observations. That’s not what this is. This is sticking fingers in a dike that doesn’t hold water. Flat earthers should object. But they never do.

10. Apply the scientific method

I happen to know that flat-earthers respect the scientific method, and I certainly do not wish for this section title to be construed as insulting or accusatory. I think almost everyone is aware of science’s unprecedented power to winnow grain from chaff. John Snow’s cholera map led to improved sanitation and the saving of countless lives and endless grief and misery. Marie and Pierre Curie’s investigations cracked open the atom’s nucleus and opened a new realm of medical science. Cecilia Payne-Gaposchkin’s dissertation research fingered hydrogen as the most abundant element in the universe despite its scarcity on earth.

That said, and with all due respect: Flat-earthers, you’re not doing it right.

History is littered with ideas that now seem quaint. Martian canals. Phrenology. Luminiferous ether. Spontaneous generation of life. When relevant data came along, these ideas were dropped. By “came along,” I mean that highly motivated individuals invested huge amounts of imagination, creativity, and physical drive to advance the current state of knowledge. Key to this process is that the community, the scientific community and the larger community, ingested the new data and revised their world model in accordance.

The missing step for flat-earthers is the part where one rejects models that don’t match reality. That step takes courage. That step takes honesty. That step takes integrity.

I haven’t seen it happen . . . yet.

But I have hope.

---

---

---

1. The also-very-popular alt-az mount is cheaper than an equatorial mount for the same size ‘scope. One might argue that cheaper equates to observer-friendly, and so an extent that is true, hence the popularity of the Dobsonian mount. Also, polar-aligning your portable telescope is time-consuming and often frustrating. That said, though, having that star just stay in the field of view without having to adjust the telescope every 60 seconds is priceless. Also, astrophotography is nigh impossible without an equatorial mount. ↩︎
2. The calculation is simply the inverse-tangent of [4800/(3/4 of the total width of the model)]. Hold your fist out at arm’s length. The angular distance across your knuckles is about 10 degrees. The sun can never approach the horizon as closely as 1.7 fists. ↩︎